PROPORCION AUREA

construccion de una mano mecanica, apartir de la proporcion aurea, con pitillos y cuerda
Esta proporción ha fascinado desde hace siglos al ser humano, que lo ha considerado un indicador de la perfección y la estética.
En el Renacimiento, muchísimos artistas y arquitectos compusieron sus trabajos con la intención de aproximarse a la proporción Áurea, convencidos de que esta relación atribuía a las obras un
carácter estético especial.

El ejemplo más cercano y curioso en el que encontraremos la proporción áurea es en las tarjetas de crédito. Si dividimos el ancho entre el alto de una tarjeta de crédito obtendremos el número
áureo: 1,618 .
Esta fascinación y mitificación de la proporción áurea continúa viva en nuestros días, y es precisamente en el diseño de logotipos donde encontramos grandes ejemplos de ello.
Creyendo que la proporción áurea ayudará a crear diseños estéticamente más agradables, muchos creativos han optado por aplicar esta relación a la construcción de sus logotipos.
 Por ejemplo,
observamos esta relación áurea en el logotipo de Apple, uno de los iconos más reconocible de nuestro siglo. Su diseño, limpio y proporcionado, está además construido en función a una serie de
circunferencias, cuya relación encaja perfectamente en la proporción áurea.
Por ejemplo,
observamos esta relación áurea en el logotipo de Apple, uno de los iconos más reconocible de nuestro siglo. Su diseño, limpio y proporcionado, está además construido en función a una serie de
circunferencias, cuya relación encaja perfectamente en la proporción áurea.

El segundo ejemplo que nos encontramos es el del logotipo de National Geographic, diseñado por el estudio neoyorkino Chermayeff & Geismar (http://www.cgstudionyc.com/identities/national-geographic). Aunque en apariencia parezca un simple rectángulo amarillo, en realidad este rectángulo respeta a la perfección las proporciones áureas. Un detalle muy apropiado para una marca centrada en la belleza de la naturaleza.

En el logotipo de Toyota podemos observar fácilmente esta divina proporción. Enmarcando el logotipo en una cuadrícula, se aprecia que las relaciones entre las distintas distancias resultantes es siempre 1,618, el número áureo.

Curiosamente en el nuevo logotipo de Pepsi, diseñado por the Arnell Group (http://www.arnellgroup.com/) en 2008, también presenta la divina proporción entre las dos circunferencias que lo conforman.

El logotipo de iCloud, uno de las últimas identidades presentadas por Apple, también respeta las proporciones áureas. La relación entre los círculos, así como la relación entre el ancho y el alto del logo, es de 1,618, el número áureo.

El rediseño de BP, llevado a cabo por Landor Associates (http://landor.com/#!/work/case-studies/bp/) en 2001, presentó una estructura de círculos concentricos cuya relación era el número áureo. Es un guiño muy apropiado para el caso ya que uno de los principales objetivos de Landor con este proyecto fue el de potenciar los valores de naturaleza y cuidado medio ambiental.

El logotipo de Grupo Boticario fue creado por la oficina brasileña de Futurebrand (http://www.futurebrand.com/work). Es quizás uno de los casos más obvios en los que encontramos las proporciones áureas.

Pero quizás uno de los logos más recientes en presentar las supuestas proporciones áureas en su diseño ha sido el nuevo icono de Twitter. Pero lo más curioso de todo esto es cómo la propia web de
Twitter presenta una estructura compuesta en función a la divina proporción.

CREAR UNA PROPOCION AURE CON UN PAPEL
Número de oro
El número áureo es la relación o proporción que guardan entre sí dos segmentos de rectas. Fue descubierto en la antigüedad, y puede encontrarse no solo en figuras geométricas, sino también en la naturaleza. A menudo se le atribuye un carácter estético especial a los objetos que contienen este número, y es posible encontrar esta relación en diversas obras de la arquitectura u el arte
El descubrimiento de este número se atribuye a la escuela Pitagórica, de hecho los pitagóricos utilizaban como símbolo la estrella de cinco puntas, en la que aparecen distintas razones áureas.
Es fácil encontrar distintas proporciones áureas en diversas figuras. Este número aparece repetidamente en el mundo que nos rodea, como elemento de diseño en construcciones arquitectónicas tan antiguas como la pirámide de Keops, o en distintos seres vivos, tanto en el reino vegetal (flores, semillas,...) como en el reino animal (estrellas de mar, caracolas que crecen en función de relaciones áureas,...) Leonardo da Vinci en su "Esquema de las proporciones del cuerpo humano" señala distintas relaciones áureas que existen en el ser humano.
El primero en hacer un estudio formal sobre el número áureo fue Euclides, unos tres siglos antes de Cristo, en su obra Los Elementos. Euclides definió su valor diciendo que "una línea recta está dividida en el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor."
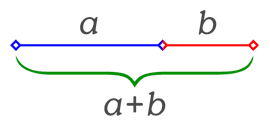
Se divide un segmento cualquiera en dos partes de forma que la razón entre la totalidad del segmento y una parte (la mayor) sea igual a la razón entre esta parte y la otra (la menor).

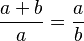
Esta razón, que cumple la propiedad, es denominada razón áurea. Se puede obtener este número a partir de la expresión anterior:

Se puede despejar a utilizando la fórmula general de las ecuaciones de segundo grado, teniendo en cuenta que a > 0 y b > 0, o en otras palabras, tomando su valor positivo:

Dividiendo todo por b se obtiene:
 . El valor de esta relación es un número que, como también demostró Euclides,
no puede ser descrito como la razón de dos números enteros (es decir, es irracional y posee infinitos decimales) cuyo su valor aproximado es 1,6180339887498...
. El valor de esta relación es un número que, como también demostró Euclides,
no puede ser descrito como la razón de dos números enteros (es decir, es irracional y posee infinitos decimales) cuyo su valor aproximado es 1,6180339887498...
- La razón o cociente entre un término y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo. Es decir:
- Este límite no es privativo de la Sucesión de Fibonacci. Cualquier sucesión recurrente de orden 2, como la sucesión 3, 4, 7, 11, 18,..., lleva al mismo límite. Esto fue demostrado por Barr y Schooling en una carta publicada en la revista londinense "The Field" del 14 de diciembre de 1912. Los cocientes son oscilantes; es decir, que un cociente es menor al límite y el siguiente es mayor. Los cocientes pueden ordenarse en dos sucesiones que se aproximan asintóticamente por exceso y por defecto al valor límite.
- Cualquier número natural se puede escribir mediante la suma de un número limitado de términos de la sucesión de Fibonacci, cada uno de ellos distinto a los demás. Por ejemplo, 17 = 13 + 3 + 1, 65 = 55 + 8 + 2.
- Tan sólo un término de cada tres es par, uno de cada cuatro es múltiplo de 3, uno de cada cinco es múltiplo de 5, etc. Esto se puede generalizar, de forma que la sucesión de Fibonacci es periódica en las congruencias módulo m, para cualquier m.

- Cada número de Fibonacci es el promedio del término que se encuentra dos posiciones antes y el término que se encuentra una posición después. Es decir
- En la pág. 61 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el conservador del museo del Louvre, Jacques Saunière.
- En el álbum Lateralus de la banda estadounidense Tool, los patrones de la batería (Danny Carey) de la canción "Lateralus" siguen la Sucesión de Fibonacci del número 13 (número de pistas del disco): 1,1,2,3,5,8,13,1,1,2,3,5,8,13,1,1,...
- En la miniserie Taken, la Sucesión de Fibonacci, como la Ecuación de Dios, es descubierta en los planes de los extraterrestres, en ejemplos como que sus naves tienen 5 tripulantes, sus manos 3 dedos y un pulgar, 1597 avistamientos ovnis en año anterior, se siguieron a 55 parejas para descubrir la híbrida humano-extraterrestre Allie, y que finalmente el número de abducidos era de 46368. Incidentalmente se habla en de un hombre que fue abducido 13 veces. 1, 3, 5, 13, 55, 1597, 46368, todos números Fibonacci.
- En el filme de Darren Aronofsky π el orden del caos el judío Rabbi Cohen presenta la teoría en hebreo transcrito en números en la cual el personaje Max Cohen relaciona esta última teoría con la secuencia de Fibonacci llegando en conclusión que todo esta basado en la ley del orden y el caos.
- En un lateral de la cúpula de la antigua sinagoga ahora convertida en el Museo Nazionale del Cinema, más conocida como Mole Antonelliana, en Torino (Italia), se puede observar una instalación luminosa de la sucesión de números de Fibonacci.
- El Dr. Walter Bishop de la serie de televisión Fringe usa números de la serie de Fibonacci para las contraseñas de sus cajas de seguridad. Capítulo 10 de la primera temporada.
- En el videojuego de Assasins Creed 2, en uno de los acertijos de los glifos para resolverlo se debe usar la sucesión de Fibonaccci para poder resolverlo.
- En el juego móvil Doom RPG hay una habitación secreta que requiere de los primeros 7 dígitos de la sucesión de Fibonacci (11235813) para poder desbloquearla.
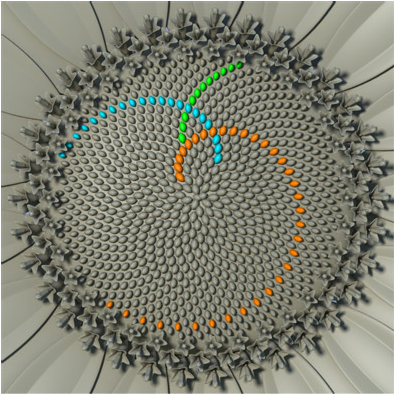
La sucesión de Fibonacci en la naturaleza
|
Si vamos dividiendo cada valor de la Serie de Fibonacci por el anterior, el resultado tiende a Phi. Cuanto más altos son los valores, mayor es la aproximación (considerad que Phi,
como todo número irracional, tiene infinitos decimales).
|

|

Y hacemos un cuadriculado con estos números, con cada cuadrito con el valor de 1 obtendríamos algo
así
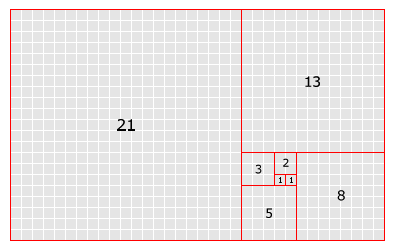
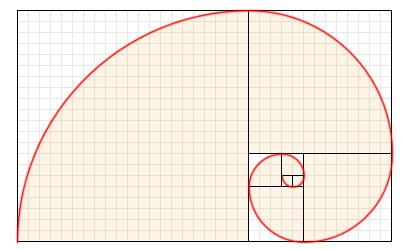
Y podemos ver estas espirales en la naturaleza como en creaciones humanas


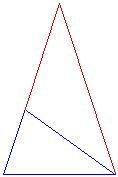
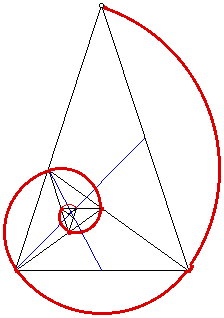
Es un triángulo isósceles especial. El ángulo superior es de 36 ° mientras que la parte inferior dos ángulos de 72 ° cada uno. A continuación, atraviesan uno de estos ángulos de la base. El triángulo azul resultante:
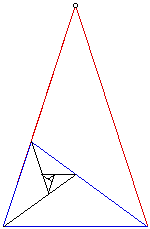


Ángulo de oro
-
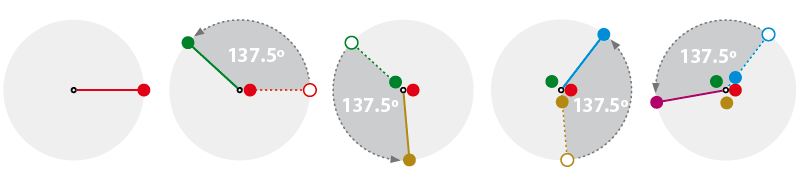
 Un concepto, quizás no tan conocido, pero igualmente importante: el Ángulo Áureo. Es decir, la relación angular de proporción entre dos segmentos circulares:
Un concepto, quizás no tan conocido, pero igualmente importante: el Ángulo Áureo. Es decir, la relación angular de proporción entre dos segmentos circulares: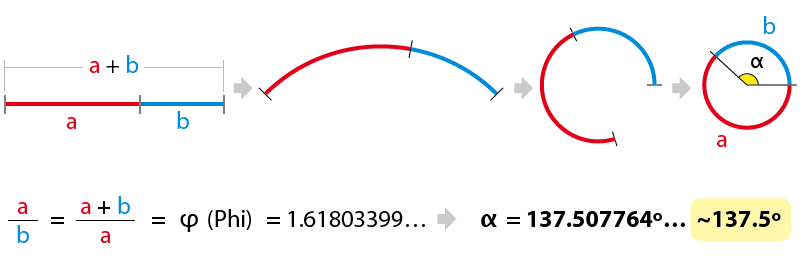

 El pentágono y el decágono, su relación con la sección aurea.
El pentágono y el decágono, su relación con la sección aurea.

Podemos encontrar el número áureo en distintos seres que pueblan la naturaleza, entre ellos el hombre. Por ejemplo, las caracolas crecen en función de relaciones áureas lo mismo que las piñas o las hojas que se distribuyen en el tallo de una planta. Las falanges de nuestra mano guardan esta relación, lo mismo que la longitud de la cabeza y su anchura.
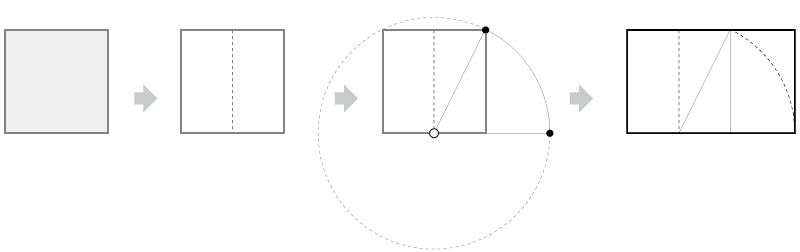
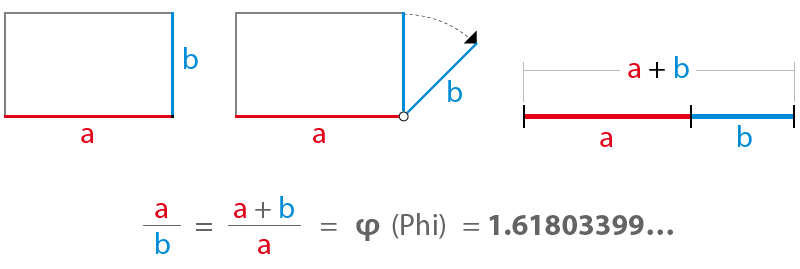
Si tomamos un
rectángulo áureo ABCD y le sustraemos el cuadrado AEFD cuyo lado es el lado menor AD del rectángulo, resulta que el rectángulo EBCF es áureo. Si después a éste le quitamos el cuadrado EBGH, el
rectángulo resultante HGCF también es áureo. Este proceso se puede reproducir indefinidamente, obteniéndose una sucesión de rectángulos áureos encajados que convergen hacia el vértice O de una
espiral logarítmica.

Esta curva ha
cautivado, por su belleza y propiedades, la atención de matemáticos, artistas y naturalistas. Se le llama también espiral equiangular (el ángulo de corte del radio vector con la curva es
constante) o espiral geométrica (el radio vector crece en progresión geométrica mientras el ángulo polar decrece en progresión aritmética). J. Bernoulli, fascinado por sus encantos, la llamó
spira mirabilis, rogando que fuera grabada en su tumba.

La espiral logarítmica vinculada a los rectángulos áureos gobierna el crecimiento armónico de muchas formas vegetales (flores y frutos) y animales (conchas de moluscos), aquellas en las que la
forma se mantiene invariante. El ejemplo más visualmente representativo es la concha del nautilus.

Leonardo Da Vinci
realizó este dibujo para ilustrar el libro De Divina Proportione del matemático Luca Pacioli editado en 1509. En dicho libro se describen cuales han de ser las proporciones de las construcciones
artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean las del dibujo adjunto. Resulta que la relación entre la altura
del hombre y la distancia desde el ombligo a la mano es el número áureo.

En el cuerpo
humano el número áureo aparece en muchas medidas: la relación entre las falanges de los dedos es el número áureo, la relación entre la longitud de la cabeza y su anchura es también este
número.

En la oreja

En la boca

Según se sabe,
una vez inseminada la abeja reina por un zángano (de otro enjambre), aquella se queda en su colmena y ya no sale más, dedicándose a la puesta de huevos que ella misma va fecundando o no, dando
origen así a abejas obreras, o bien reinas, en el primer caso y machos o zánganos en el segundo. Si observamos el árbol genealógico (figura 1) de un zángano, podemos ver como el número de
abejas en cada generación es uno de los términos de la sucesión de Fibonacci.
La serie de
FIbonacci se puede encontrar también en botánica. Así, por ejemplo, ciertas flores tienen un número de pétalos que suelen ser términos de dicha sucesión; de esta manera el lirio tiene 3 pétalos,
algunos ranúnculos 5 o bien 8, las margaritas y girasoles suelen contar con 13, 21, 34, 55 o bien 89.

La parte de la
botánica que estudia la disposición de las hojas a lo largo de los tallos de las plantas se denomina Filotaxia. En la mayoría de los casos es tal que permite a las hojas una captación uniforme de
la luz y aire, siguiendo, normalmente, una trayectoria ascendente y en forma de hélice.

Si tomamos la
hoja de un tallo y contamos el número de hojas consecutivas (supongamos que son 'n') hasta encontrar otra hoja con la misma orientación, este número es, por regla general, un término de la
sucesión de Fibonacci. Además, si mientras contamos dichas hojas vamos girando el tallo (en el sentido contrario a las agujas del reloj, por ejemplo) el numero de vueltas 'm' que debemos dar a
dicho tallo para llegar a la siguiente hoja con la misma orientación resulta ser también un término de la sucesión. Pues bien, se llama "característica" o "divergencia" del tallo a la fracción
m/n, y que, como muestra en la figura 2, en el olmo es 1/2, en el álamo 2/5, en el sauce llorón 3/8 y en el almendro 8/13. Si representamos por Fn el término que ocupa
el lugar 'n' en la sucesión de Fibonacci (consideremos, por ejemplo: F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13), en la
mayoría de los casos la característica viene dada por una fracción del tipo Fn/Fn+2. Así, en el caso del sauce llorón sería
F4/F6.

Las "hojas" de
una piña de pino tienen, por regla general, una característica de 5/8 o bien 8/13, presentando propiedades similares las hojas de las lechugas, los pétalos de las flores, las ramas de las
palmeras, el ficus, etc., ejemplos que se pueden comprobar fácilmente.
El número áureo
ha sido utilizado desde la época de los egipcios para la construcción de edificios, si bien, son los griegos los que lo explotaron al máximo usando en todas las facetas del arte. A continuación
se detallan algunos ejemplos de este uso.

El primer uso
conocido del número áureo en la construcción aparece en la pirámide de Keops, que data del 2600 a.C..

Esta pirámide
tiene cada una de sus caras formadas por dos medios triángulos áureos: la más aparente, aunque no la única, relación armónica identificable en el análisis de las proporciones de este monumento
funerario en apariencia simple.

Un ejemplo de
rectángulo áureo en el arte es el alzado del Partenón griego.

En la figura se
puede comprobar que AB/CD= . Hay más cocientes entre sus
medidas que dan el número áureo, por ejemplo: AC/AD=
. Hay más cocientes entre sus
medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=
y CD/CA= .
.

El Templo de
Ceres en Paestum (460 a.C.) tiene su fachada construida siguiendo un sistema de triángulos áureos, al igual que los mayores templos griegos, relacionados, sobre todo, con el orden
dórico.


La Tumba Rupestre
de Mira en Asia Menor basa su construcción en un pentágono áureo, en el que el cociente de la diagonal y el lado de dicho pentágono es el número áureo.

Los lados del
rectángulo en el cual está idealmente inscrita la estatua del Apolo de Belvedere están relacionados según la sección áurea, es decir, con una proporción de 1:1,618.

El cuadro de Dalí
Leda atómica, pintado en 1949, sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica. Se trata de una filigrana basada en la proporción áurea, pero elaborada de tal forma
que no es evidente para el espectador. En el boceto de 1947 se advierte la meticulosidad del análisis geométrico realizado por Dalí basado en el pentagrama místico
pitagórico.


El número áureo
no solo lo podemos encontrar en la naturaleza o en las antiguas construcciones y representaciones artísticas, diariamente manejamos objetos en los cuales se ha tenido en cuenta las proporciones
áureas para su elaboración. Por ejemplo, la mayoría de las tarjetas de crédito así como nuestro carnet tienen la proporción de un rectángulo áureo. También lo podemos encontrar en las cajetillas
de tabaco, construcción de muebles, marcos para ventanas, camas, etc.
 Página para Fortalecer el proceso educativo,
fortalecer la educación en tecnología
y habilidades del siglo XXI
Página para Fortalecer el proceso educativo,
fortalecer la educación en tecnología
y habilidades del siglo XXI




























